An essay by Chaoran Sun ’15, Barcelona GSE Master Program in Competition and Market Regulation
Robert Aumann once complained in the foreword of Roth and Sotomayor (1992):
It is sometimes asserted that game theory is not “descriptive” of the “real world”, that people don’t behave according to game-theoretic prescriptions. To back up such assertions, some workers have conducted experiments using poorly motivated subjects, subjects who do not understand what they are about and are paid off by pittance, as if such experiments represents the real world.
Indeed, it is all too familiar for us hearing people cite Rosenthal’s centipede Game as an evidence that game theory is not “descriptive” of the “real world”. When faced with the follow-up question as to why game theory doesn’t work, they usually pointed out that it lies in game theorists’ obsession of some obviously mistaken assumptions associating with common knowledge, unbounded rationality, et cetera.
In this essay, we argue that, at least for Rosenthal’s centipede game, it’s not the case game theory is inconsistent with the findings of experiments that subjects don’t wind up on the backward induction path. To be precise, even though we accept the strong assumption of common belief of rationality, which is everyone believe everyone plays rationally, everyone believe everyone believe everyone plays rationally, ad infinitum, we shouldn’t expect backward induction path as an unavoidable outcome. The example presented here is well-known, and this essay only serves for expository purpose.
To begin, let’s have a look at technical difficulties. Since there’s no way for a player to mind-read another player, it’s absurd to assume away the possibility that one player’s subjective belief on her opponent’s strategy doesn’t coincide with the objective one1. Furthermore, we can’t stop there. What about players’ belief on their opponent’s belief, belief on beliefs on beliefs…If you wonder high-order beliefs might only have a negligible effect on the outcome of games, think about the dirty face and sage game and Rubinstein’s electronic mail game. This ever-increasing hierarchy of beliefs makes a fine line for common knowledge of game structure, the starting point of every game theory analysis, impossible. In a series of conceptual breakthroughs, Harsanyi (1967-68) postulated that this belief hierarchy can be summarized as a type so that “relaxing” the stringent requirement of common knowledge is tantamount to adding types in a game of incomplete information. It is also noteworthy that, a belief of a higher rank contains strictly more information than those of lower ranks, so it’s reasonable to require that beliefs of different ranks shan’t contradict with each other. The technical breakthrough came when Mertens and Zamir (1985) cast belief hierarchy with this coherency property into a category theory object, inverse limit and went on proving that Harsanyi universal type space attains a self-referential property, each player’s type is equivalent to a joint distribution of her opponent’s strategy and type. Now we have set the stage for the analysis of the centipede game.
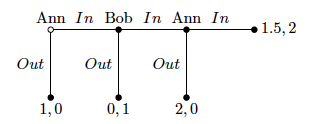
Consider a three-legged centipede game of incomplete information with Harsanyi’s universal type space. Ann of type a believes that Bob plays “In”, while Ann of type b believes that Bob plays “Out” . Bob, on the other hand believes Ann is type b and plays “Out”. Then we have:
Claim. At state (a, (In, Out), Out) whose outcome is different from backward induction path, Ann and Bob share a common belief of rationality.
What we need to verify for common belief of rationality are, at the given state:
- What Ann believes implies Ann is rational.
- What Ann believes Bob believes implies that Ann believes Bob is rational.
- What Ann believes Bob believes Ann believes implies Ann believes Bob believes Ann is rational.
. . . . . .
Notice that we only need to check the first three steps, what Ann believes Bob believes Ann believes is the same as what Ann believes Bob believes Ann believes…Bob believes Ann believes. They’re indeed the case. Next, apply the same procedure to a case with Ann and Bob interchanged.
Remark. When conducting experiments, we should be careful about how well subjects understand games they’re playing, how well they know about the opponents they’re play- ing against. Experimental findings in disfavor of backward induction might indicate that epistemic conditions for backward induction are not satisfied. Common knowledge of game structure and common belief of rationality, saving us from arbitrariness of off- equilibrium paths, could be relevant to resolving real world economic problems, if put into perspective.
References
- Aumann, Robert J. Backward induction and common knowledge of rationality. Games and Economic Behavior (1995), 6-19.
- Aumann, Robert J. On the Centipede Game. Games and Economic Behavior (1998), 97-105.
- Binmore, Ken. A Note on Backward Induction. Games and Economic Behavior (1996), 135-137.
- Harsanyi, John. Games on incomplete information played by Bayesian players. Parts I, II, III. Management Science (1967-1968), 159-182, 320-334, 486-502.
- Mertens, Jean. F. and Shmuel Zamir. Formulation of Bayesian analysis for games with incomplete information. International Journal of Game Theory (1985), 1-29.
- Roth, Alvin E., Sotomayor, Marilda A. Oliveira Two-Sided Matching: A Study in Game-Theoretic Modeling and Analysis. Cambridge University Press (1992).
- Stalnaker, Robert. Knowledge, belief and counterfactual reasoning in games. Economics and Philosophy (1996), 133-163.
1 One of central question in game theory was under what setting, common belief of rationality implies backward induction. When Aumann(1995), (1998) derive backward induction path as a consequence of common knowledge of rationality rather than common belief of rationality, it attracted a lot of criticism related to the aforementioned reasoning that knowledge, for being necessarily true, is too strong (see Binmore(1996) and Stalnaker(1996)). In this essay, when we say a player believes an event, it means that player believes that this event is obtained with probability 1.
