Editor’s note: In this post, Greg Ganics (Economics ’12 and PhD candidate at UPF-GPEFM) provides a non-technical summary of his job market paper, “Optimal density forecast combinations,” which has won the 2016 UniCredit & Universities Economics Job Market Best Paper Award.
After the recent Great Recession, major economies found themselves in a situation with low interest rates and fragile economic growth. This combination, along with major political changes in key countries (the US and the UK) makes forecasting more difficult and uncertain. As a consequence, policy makers and researchers have become more interested in density forecasts, which provide a measure of uncertainty around point forecasts (for a non-technical overview of density forecasts, see Rossi (2014)). This facilitates communication between researchers, policy makers, and the wider public. Well-known examples include the fan charts of the Bank of England, and the Surveys of Professional Forecasters of the Philadelphia Fed and the European Central Bank.
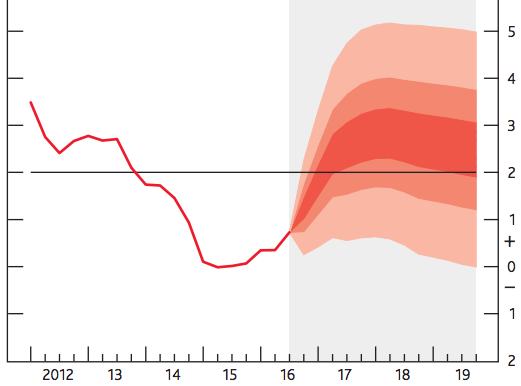
Forecasters often use a variety of models to generate density forecasts. Naturally, these forecasts are different, and therefore researchers face the question: how shall we combine these predictions? While there is an extensive literature on both the theoretical and practical aspects of combinations of point forecasts, our knowledge is rather limited about how density forecasts should be combined.
In my job market paper “Optimal density forecast combinations,” I propose a method that answers this question. My main contribution is a consistent estimator of combination weights, which could be used to produce a combined predictive density that is superior to the individual models’ forecasts. This framework is general enough to include a wide range of forecasting methods, from judgmental forecast to structural and non-structural models. Furthermore, the estimated weights provide information on the individual models’ performance over time. This time-variation could further enhance researchers’ and policy makers’ understanding of the relevant drivers of key economic variables, such as GDP growth or unemployment.
Macroeconomists in academia and at central banks often pay special attention to industrial production, as this variable is available at the monthly frequency, therefore it can signal booms and busts in a timely manner. In an empirical example of forecasting monthly US industrial production, I demonstrate that my novel methodology delivers density forecasts which outperform well-known benchmarks, such as the equal weights scheme. Moreover, I show that housing permits had valuable predictive power before and after the Great Recession. Furthermore, stock returns and corporate bond spreads proved to be useful predictors during the recent crisis, suggesting that financial variables help with density forecasting in a highly leveraged economy.
The methodology I propose in my job market paper can be useful in a wide range of applications, for example in macroeconomics and finance, and offers several avenues for further research, both theoretical and applied.
References:
Ganics, G. (2016): Optimal density forecast combinations. Job market paper
Rossi, B. (2014): Density forecasts in economics and policymaking. Els Opuscles del CREI, No. 37