Editor’s note: This post is part of a series showcasing Barcelona GSE master projects by students in the Class of 2018. The project is a required component of every master program.
Authors:
Patrick Altmeyer, Jacob Daniel Grapendal, Makar Pravosud, and Gand Derry Quintana
Master’s Program:
Paper Abstract:
There exists a substantial body of literature concerned with the calibration of the Heston model for pricing financial derivatives under stochastic volatility, many of which rely on computationally expensive algorithms. Our paper evaluates a calibration method of the Heston model proposed by Alòs, De Santiago, and Vives (2015), which can be used to price derivatives with little computational effort. The calibration method is innovative in the sense that it considers only the three most critical regions of the implied volatility surface. The regions where the underlying option is, firstly, at-the-money, secondly, close to maturity and lastly, far away from maturity. Although their procedure is parsimonious and very easy to implement, they calibrate a model whose empirical applicability is contested.
The main contribution of our paper is the evaluation of their model in an extensive numerical exercise as well as an application to real data. Collecting empirical option data has been one of the main challenges with respect to this work, since historical data on financial derivatives is not accessible to the public. Faced with this issue we have written a script that allowed us to automatically scrape option data at a high frequency over just a couple of weeks. Thus, we build our own extensive data base. Also, we have made the data and code available on https://griipen.shinyapps.io/bgse/ and https://github.com/HitKnit/BGSE2018/tree/HitKnit-optionscraping, respectively.
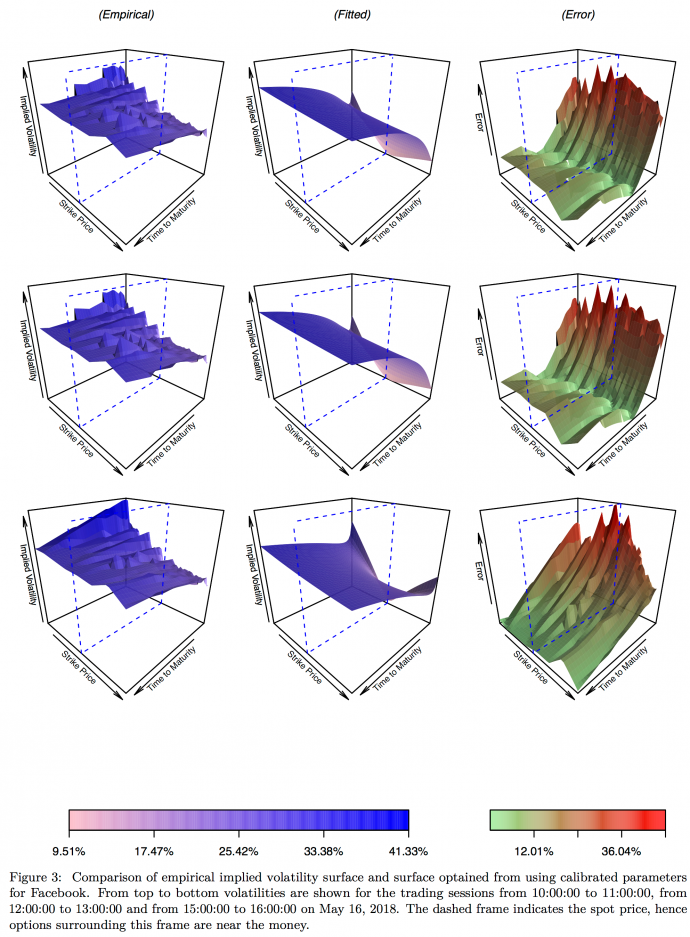
In terms of our results, we find that whilst the calibration method has solid theoretical foundations and produces satisfactory estimation results within the theoretical Heston universe. However, it fails in practice. Specifically, for the numerical exercise we find that out of all simulations the maximum average error across the entire volatility surface is 0.999 percent while the mean error across simulations is only 0.481 percent. In sharp contrast to that, absolute percentage errors for our empirical data are on the order of 30-40 percent in many cases. In the following figure, we present our findings for intra-daily data from May 16, 2018. The left column shows empirical implied volatilities for a European call option on Facebook Inc. (FB) stocks. From top to bottom volatilities are shown for the opening, lunch and closing sessions. The central column shows the fitted volatility surfaces while the right column shows absolute percentage differences between empirical and estimated values. The finding that errors are particularly high for at-the-money options with short times to maturity is robust across the entire data sample.
Conclusions and key results:
In light of these results, we conclude that inherent limitations of the Heston Model disqualify the calibration for practical use. Nonetheless, we believe that similarly simple calibration methods as the one examined here should be used in combination with more sophisticated option pricing models.
References:
Alòs, Elisa, Rafael De Santiago, and Josep Vives. 2015. “Calibration of Stochastic Volatility Models via Second-Order Approximation: The Heston Case.” International Journal of Theoretical and Applied Finance 18 (06). World Scientific: 1550036.
Download the full paper [pdf]
More about the Finance Program at the Barcelona Graduate School of Economics