Editor’s note: This post is part of a series showcasing BSE master projects. The project is a required component of all Master’s programs at the Barcelona School of Economics.
Abstract
Crossed random effects models are additive models that relate a response variable (e.g. a rating) to categorical predictors (e.g. customers and products). They can for example be used in the famous Netflix problem, where movie ratings of users should be predicted based on previous ratings. In order to apply statistical learning in this setup it is necessary to efficiently compute the Cholesky factor L of the models precision matrix. In this paper we show that for the case of 2 factors the crucial point to this end is not only the overall sparsity of L, but also the arrangement of non-zero entries with respect to each other. In particular, we express the number of flops required for the calculation of L by the number of 3-cycles in the corresponding graph. We then introduce specific designs of 2-factor crossed random effects models for which we can prove sparsity and density of the Cholesky factor, respectively. We confirm our results by numerical studies with the R-packages Spam and Matrix and find hints that approximations of the Cholesky factor could be an interesting approach for further decrease of the cost of computing L.
Key findings
- The number of 3-cycles in the fill graph of the model are an appropriate measure of the computational complexity of the Cholesky decomposition.
- For the introduced Markovian and Problematic Design we can prove sparsity and density of the Cholesky Factor, respectively.
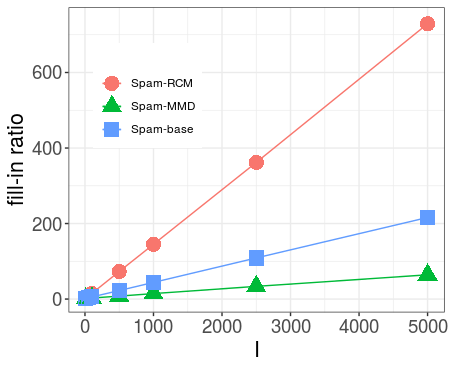
- For precision matrices created according to a random Erdös-Renyi-scheme the Spam algorithms could not find an ordering that would be significantly fill-reducing. This indicates that it might be hard or even impossible to find a general ordering rule that leads to sparse Cholesky factors.
- For all observed cases, many of the non-zero entries in the Cholesky factor are either very small or exactly zero. Neglecting these small or zero values could spare computational cost without changing the Cholesky factor ‘too much’. Approximate Cholesky methods should therefore be included in further research.
Connect with the author
- Maximillian Müller: LinkedIn
